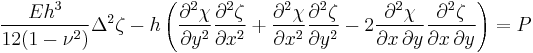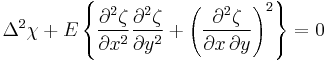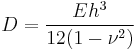Föppl–von Kármán equations

The Föppl–von Kármán equations, named after August Föppl[1] and Theodore von Kármán,[2] are a set of nonlinear partial differential equations describing the large deflections of thin flat plates.[3] With application ranging from the design of submarine hulls to the mechanical properties of cell wall,[4] the equations are notoriously difficult to solve, and take the following form: [5]

\frac{Eh^3}{12(1-\nu^2)}\Delta^2\zeta-h\frac{\partial}{\partial x_\beta}\left(\sigma_{\alpha\beta}\frac{\partial\zeta}{\partial x_\alpha}\right)=P
\frac{\partial\sigma_{\alpha\beta}}{\partial x_\beta}=0

where

E = Young's modulus
\sigma_{\alpha\beta} = Stress tensor
h = Thickness of the plate
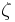\zeta = Out of plane deflection
\nu = Poisson's ratio
P = External normal force per unit area of the plate
\Delta = 2-dimensional Laplacian

Introducing the Airy stress function 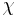\chi the above equations become[5]

\frac{Eh^3}{12(1-\nu^2)}\Delta^2\zeta-h\left(\frac{\partial^2\chi}{\partial y^2}\frac{\partial^2\zeta}{\partial x^2}%2B\frac{\partial^2\chi}{\partial x^2}\frac{\partial^2\zeta}{\partial y^2}-2\frac{\partial^2\chi}{\partial x \, \partial y}\frac{\partial^2\zeta}{\partial x \, \partial y}\right)=P
\Delta^2\chi%2BE\left\{\frac{\partial^2\zeta}{\partial x^2}\frac{\partial^2\zeta}{\partial y^2}%2B\left(\frac{\partial^2\zeta}{\partial x \, \partial y}\right)^2\right\}=0

Pure bending

For the pure bending of thin plates the equation of equilibrium is 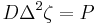D\Delta^2\zeta=P, where

D=\frac{Eh^3}{12(1-\nu^2)}

is called flexural or cylindrical rigidity of the plate.[5]

References

  1. ^ Föppl, A., "Vorlesungen über technische Mechanik", B.G. Teubner, Bd. 5., p. 132, Leipzig, Germany (1907)
  2. ^ von Kármán, T., "Festigkeitsproblem im Maschinenbau," Encyk. D. Math. Wiss. IV, 311–385 (1910)
  3. ^ E. Cerda and L. Mahadevan, 2003, "Geometry and Physics of Wrinkling" Phys. Rev. Lett. 90, 074302 (2003)
  4. ^ http://focus.aps.org/story/v27/st6
  5. ^ a b c "Theory of Elasticity". L. D. Landau, E. M. Lifshitz, (3rd ed. ISBN 075062633X)
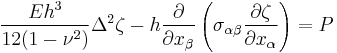
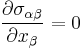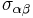